デジタル再生では元の2倍のサンプリング(2・fs)が有れば元の信号を再現出来ると云われて周波数特性ば話題に上がっても 質については あまり聞いた事が有りません。
CDの44.1KHzとDXDの384KHzの差は周波数特性によるのかな~
CDとDXDでは量子化bit数の差が有りますがサンプリング周波数の差も無視できないので1周期内のサンプル数(∽周波数)を変化させた時どうなるのか見てみました。
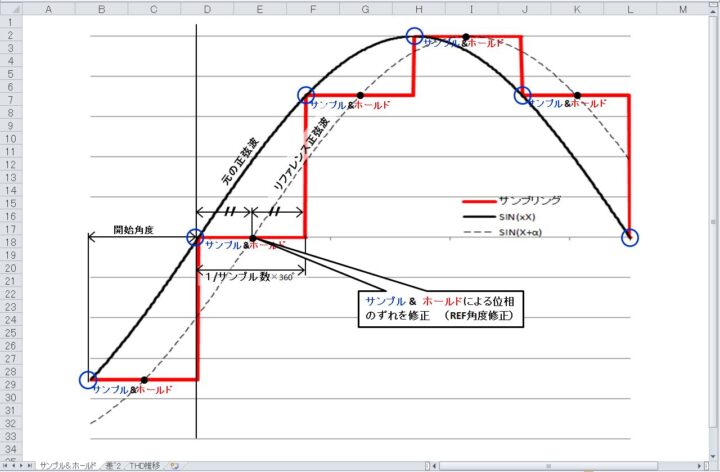
NETでよく見るサンプリング波形ををEXCELの散布図で再現しました。
・サンプル数は1周期に何回サンプルするかでサンプリング周波数/20KHzの倍率に相当します。
・黒線が「元の正弦波」で赤線が「サンプル&ホールドの波形」です。
・DACの動作に倣って赤線の「サンプル&ホールドの波形」はサンプルのタイミングの正弦波の値を次のタイミングまで保持(ホールド)するようにしました。
・開始角度はサンプルをどのタイミングで開始するかで、録音時はランダムに変わります。
・黒破線の「リファレンスの正弦波」はサンプル&ホールドで元の正弦波から位相(時間)がずれるので 修正の為にホールド時間の1/2シフトしています。
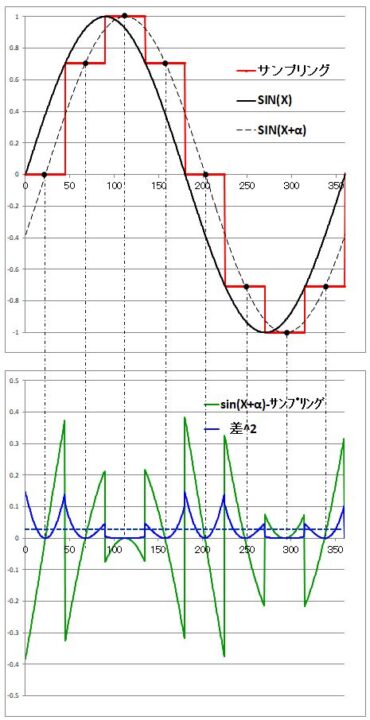
「サンプル&ホールドの波形」から「THD」の算出は難しいので代案として
「差」=「リファレンスの正弦波」-「サンプル&ホールドの波形」を計算
「差」を2乗して青線の「差^2」に さらに”√「差^2の平均値」/実効値”を計算して「面積差^2」としました。
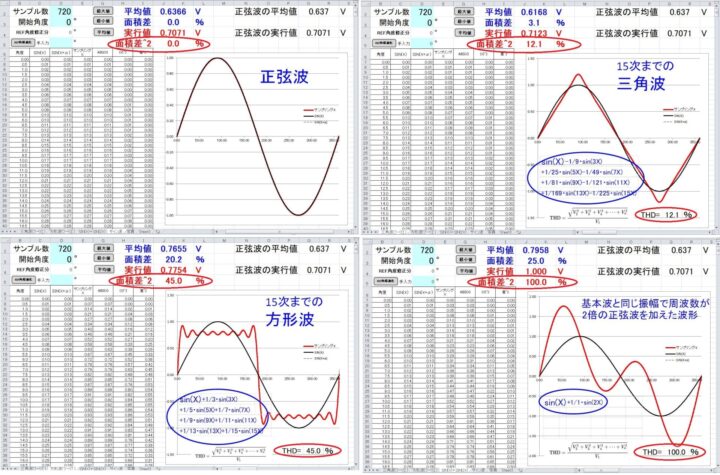
「面積差^2」の有効性を調べる為に「サンプル&ホールドの波形」のデーター部分に次の4種類の波形をセットして「THD」と比較しました。
※サンプル&ホールドしていないので開始角度・REF角度修正は共に0です。
1.波高値が1V(実効値=0.7071V)の基本波のみ=「元の正弦波」(THD=0%)
2.基本波の波高値が1Vで15次までの三角波と方形波
3.基本波と同じ振幅で周波数が2倍の正弦波を加算した波形(THD=100%)
Wikipediaによれば「THD」は
波形作成に使った級数の各高調波(15次まで)の実効値を求めて「THD」を計算しました。
4種類の波形です。
「THD」と「面積差^2」をまとめると
「THD」 「面積差^2」
正弦波 0% 0%
三角波(15次まで) 12.1% 12.1%
方形波(15次まで) 45.0% 45.0%
sin(X)+sin(2X) 100% 100%
元になった波形が同じなら計算方法が違っても「THD」と「面積差^2」は一致するみたいです。
「THD」が計算出来なくても「元の正弦波」と「調べる波形」が解かれば「面積差^2」が使えそうです。・・・何を持って「元の正弦波」とするかが難しいですが!
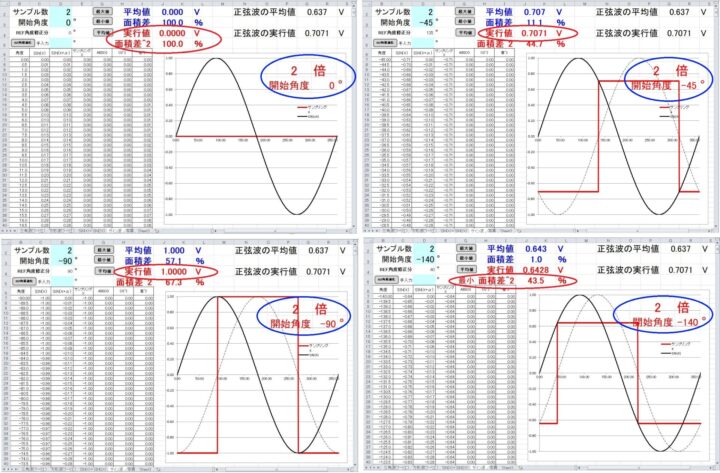
最低限と云われる2・fsのサンプル数=2でサンプリングの開始角度=0°,-45°,-90°と角度を0~-180°変えた時の「面積差^2」の最小値を計算をしました。
1.実効値は開始角度=0°で”0V” ~ -90°で”1V”となんでも有りです。
2.「面積差^2」は最小43%~最大100%まで変わりました。
一見高さの違う方形波に見えますが、この方形波から波高値=1Vの「元の正弦波」を再現するのは とっても難しそうです。
このままでは比較出来ないので、開始角度を0~-180°変えた時の「面積差^2」の平均を求めました。表示は平均値と一致する角度をVLOOKUP関数で逆算しています。
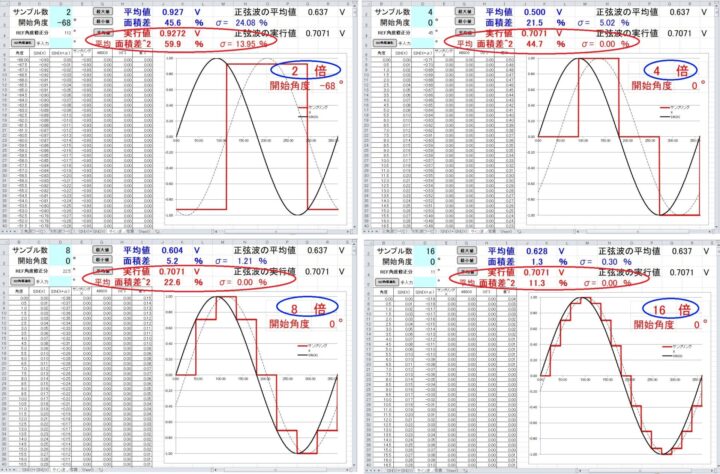
サンプル数を2,4,8,16と上げた時の実効値と「面積差^2」の平均の変化を見ました。
これ本当? 桁が違うのではと思われる結果ですが、サンプル数が少ないと正弦波より方形波に近い波形なので当たらすとも遠からずでしょう・・・か?
1.サンプル数が大きくなるほど「面積差^2」は小さくなりました。
2.サンプル数が4以上で実効値の変化は無くなりました。
3.同じく4以上になると 開始角度による「面積差^2」の変動は無く(σ=0)なりました。
サンプル数が4(80KHz=20KHz×4)以上有れば実効値が変わらないので周波数特性は~20KHzまで良好と判断出来ますが問題はその質です。
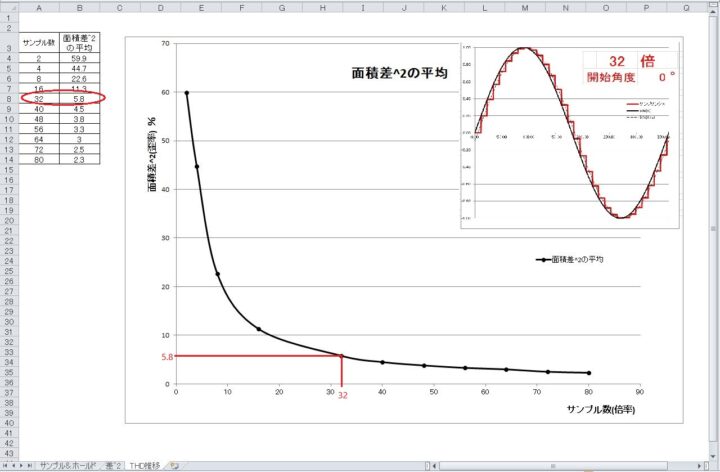
そこでサンプル数と「面積差^2」の推移をグラフ化しました。
これを見るとサンプル数が32までは急激に下がりますがそれ以降の変化は小さいです。
640KHz = 20KHz × 32
「面積差^2」= 5.8%
384KHzのDXDより高い周波数の640KHzで「面積差^2」= 5.8%になりました。
波形も32倍になるとそれらしくなりギザギザは多いですが正弦波に見えます。
逆に見るとCDは22KHz~1.4KHz(=44.1KHz/32)までサンプリングの影響が色濃く出るかもです。
低次高調波の多いアナログ的な歪と異なり 聴こえない高次高調波の多いDA変換信号の「THD」が聴感上どの程度影響するかは不明ですが、「面積差^2」が急激に下がる周波数のDXDは思った以上に効果が有りそうです。
—————————————————————————–
以前にパソコンで歪率を測定をして「philm-community」に投稿した時に

NETで調べた理論歪率は7次までで
理論値 表示(Flat topで測定)
方形波 41% —>43% 誤差5%
三角波 10.3%—>11.9% 誤差15%
微妙な結果でした。
今回15次まで計算したので理論値に当てはめると
理論値 表示
方形波 45.0%—>43% 誤差4%
三角波 12.1%—>11.9% 誤差2%
とっても良い結果になりました。



コメント ※編集/削除は管理者のみ
DA変換の波形はサンプルホールドではなくローパスフィルタでfs/2以上の成分をカットした波形と比較しないと見誤ります。
NOSなどの特殊なDACでなければオーバーサンプリングしてデジタルフィルタで高域をカットしたいるはずですのでそれと比較するべきです。
Qiitaに書いた記事のリンクです。自分のブログじゃないから良いよね? 問題あればここにも同じ記事をアップしますがあまりこのサイト向きではないかも。
https://qiita.com/assi-dangomushi/items/8b7f8bd851ecce9abe87
https://qiita.com/assi-dangomushi/items/63ebcbcf070080784e6a
https://qiita.com/assi-dangomushi/items/89b360755c8c4359b7ee
assiさん
確かにフィルターを通すと見た目は大きく変わりますが問題は聴こえない領域の特性でなく日記にも書いた
>逆に見るとCDは22KHz~1.4KHz(=44.1KHz/32)までサンプリングの影響が色濃く出るかもです。
の可聴帯域の方だと思っています。
1.4KHzで無視出来ない歪が有れば20KHzの理想的なフィルターを入れても14倍の帯域となりギザギザ分の可聴帯域分を十分通すのではと考えます。
これが~20KHzの全帯域で起こると 上に行く程歪分は大きくなるのでその影響は無視出来ないと思います。
いやいや、高域をカットした状態で、可聴帯域の波形に変化があるかを調べるべきという話です。高域をカットすればそもそもギザギザがなくなってしまいす。CDの再生波形はギザギザではないのです(NOSを除く)。
CD聴いていて感じる微小領域の歪感は16bitフルに使った話では無くて数bitの話だと思います。
極端な場合の最小の1bitだといくら頑張っても方形波
1.4KHzの数bitをデジタルフィルターで補間しても立ち上がりの一部だけで大半は変形方形波になるかと・・・
これを更に20KHzの理想フィルターを通してもあまり変わらないと思います。
いままでサンプリング周波数UPによる広帯域化の話ばかりで可聴帯域内の歪の話はあまり無かったと思います。
理解しました。サンプリング周波数の問題ではなくbit深度が足りない場合の量子化歪についての話だったのですね。たしかに量子化bit数が少ない場合には歪が多く出ます。これはサンプリング周波数を上げれば改善しますがbit深度を24bitにすればサンプリング周波数が44.1kHzのままでも更に改善します。
私も16bitでは余裕がない(そうは言っても十分高音質ですが)と感じるのですが24bitあれば十分に量子化ノイズは少ないと思ってます。
今まで可聴帯域内の歪に関する考察かあまり無くて何とか問題提起したいと思い今回の日記になりました。
耳の感度か最も高い3KHzはCDのサンプリング周波数で問題ないと思っていましたが、歪率の観点から見ると決して小さくない歪があるようです。
実際に384KHzのDXDを聴くと全く別物の感じるのはこうした事も要因の一つに上げられると思います。
384KHzを192KHzにダウンコンバートした物でも「どうしてこんなに違うの、CDと96KHzの差より違いが大きいのでは?」とか「リマスタリングみたいな事をしていなか?」と云った意見があるくらいです。